|
|
 有效数字 有效数字 |
|
所謂有效數字:具體地說,是指在分析工作中實際能夠測量到的數字。所謂能夠測量到的是包括最後一位估計的,不確定的數字。
我們把通過直讀獲得的準確數字叫做可靠數字;把通過估讀得到的那部分數字叫做存疑數字.把測量結果中能夠反映被測量大小的帶有一位存疑數字的全部數字叫有效數字.如上例中測得物體的長度7.45cm.數據記錄時,我們記錄的數據和實驗結果的表述中的數據便是有效數字. |
|
測量結果都是包含誤差的近似數據,在其記錄、計算時應以測量可能達到的精度為依據來確定數據的位數和取位。如果參加計算的數據的位數取少了,就會損害外業成果的精度並影響計算結果的應有精度;如果位數取多了,易使人誤認為測量精度很高,且增加了不必要的計算工作量。
一般而言,對一個數據取其可靠位數的全部數字加上第一位可疑數字,就稱為這個數據的有效數字。
一個近似數據的有效位數是該數中有效數字的個數,指從該數左方第一個非零數字算起到最末一個數字(包括零)的個數,它不取决於小數點的位置。 |
|
1、有效數字中衹應保留一位欠準數字,因此在記錄測量數據時,衹有最後一位有效數字是欠準數字。
2、在欠準數字中,要特別註意0的情況。0在數字之間與末尾時均為有效數字。如0.078和0.78與小數點無關,均為兩位。506與220均為三位。
3、л等常數,具有無限位數的有效數字,在運算時可根據需要取適當的位數。 |
|
(1)實驗中的數字與數學上的數字是不一樣的.如
數學的 8.35=8.350=8.3500 ,
而實驗的 8.35≠8.350≠8.3500.
(2)有效數字的位數與被測量的大小和儀器的精密度有關.如前例中測得物體的長度為7.45cm,若用千分尺來測,其有效數字的位數有五位.
(3)第一個非零數字前的零不是有效數字.
(4)第一個非零數字開始的所有數字(包括零)都是有效數字.
(5)單位的變換不能改變有效數字的位數.因此,實驗中要求盡量使用科學計數法表示數據.如100.2m可記為0.1002km.但若用cm和mm作單位時,數學上可記為10020cm和100200mm,但卻改變了有效數字的位數.采用科學計數法就不會産生這個問題了. |
|
有效數字的末位是估讀數字,存在不確定性.一般情況下不確定度的有效數字衹取一位,其數位即是測量結果的存疑數字的位置;有時不確定度需要取兩位數字,其最後一個數位纔與測量結果的存疑數字的位置對應.
由於有效數字的最後一位是不確定度所在的位置,因此有效數字在一定程度上反映了測量值的不確定度(或誤差限值).測量值的有效數字位數越多,測量的相對不確定度越小;有效數字位數越少,相對不確定度就越大.可見,有效數字可以粗略反映測量結果的不確定度. |
|
 有效数字的舍入规则 有效数字的舍入规则
2、當保留n位有效數字,若後面的數字大於第n位單位數字的0.5 ,則第位數字進1。
3、當保留n位有效數字,若後面的數字恰為第n位單位數字的0.5 ,則第n位數字若為偶數時就捨掉後面的數字,若第n位數字為奇數加1。
如將下組數據保留三位
45.77=45.8 43.03=43.0
38.25=38.3 47.15=47.2
效數字:是指從該數字左邊第一個非0的數字到該數字末尾的數字個數。 |
|
| 1定義:在一個近似數中,從左邊第一個不是0的數字起,到精確到位數止,所有的數字,都叫這個近似數字的有效數字。 |
|
 有效数字的舍入规则 有效数字的舍入规则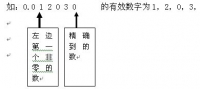 有效数字的舍入规则 有效数字的舍入规则
2、當保留n位有效數字,若後面的數字大於第n位單位數字的0.5 ,則第位數字進1。
3、當保留n位有效數字,若後面的數字恰為第n位單位數字的0.5 ,則第n位數字若為偶數時就捨掉後面的數字,若第n位數字為奇數加1。
如將下組數據保留三位
45.77=45.8 。 43.03=43.0
38.25=38.2 。 47.15=47.2
有效數字
就是一個數從左邊第一個不為0的數字數起到精確的數位止,所有的數字(包括0,科學計數法不計10的N次方),稱為有效數字。簡單的說,把一個數字前面的0都去掉,從第一個正整數到精確的數位止所有的都是有效數字了。
如:0.0109,前面兩個0不是有效數字,後面的109均為有效數字(註意,中間的0也算)。
3.109*10^5(3.109乘以10的5次方)中,3 1 0 9均為有效數字,後面的10的5次方不是有效數字
5200000000,全部都是有效數字。
0.0230,前面的兩個0不是有效數字,後面的230均為有效數字(後面的0也算)
1.20有3個有效數字
1100.024有7個有效數字
2.998*10^4(2.998乘以10的4次方)中,保留3個有效數字為3.00*10^4
整體遵循四捨六入五成雙的方法
計算規則
1. 加減法
先按小數點後位數最少的數據保留其它各數的位數,再進行加減計算,計算結果也使小數點後保留相同的位數。
例:計算50.1+1.45+0.5812=?
修約為:50.1+1.4+0.6=52.1
2. 乘除法
先按有效數字最少的數據保留其它各數,再進行乘除運算,計算結果仍保留相同有效數字。
例:計算0.0121×25.64×1.05782=?
修約為:0.0121×25.6×1.06=?
計算後結果為:0.3283456,結果仍保留為三位有效數字。
記錄為:0.0121×25.6×1.06=0.328
例:計算2.5046×2.005×1.52=?
修約為:2.50×2.00×1.52=? |
|
有效數字
significant figure
有效數字f鈎,i五咖t石,獷e或sj,訪cant崛t;3。明。-
山朋從H咖a」
用於近似確定一個實數(real number)的術語.
設實數x在基為q的數係中由q進分數表示為
x二x‘=(“。…:,“0,“一,“一:“‘:一。)·
假定在此表示式中“,是從左面數起第一個不等於零
的數字,則所有後繼數字稱為近似數x‘的有效數字.
一個有效數字“。稱為準確的(c orrect),如果x‘
的絶對誤差△(x’)即差!x一x‘l滿足不等式
△(;’)、鼕。!.
_、,2
近似確定一實數通常僅意味着確定它的有效數字.
X.八.HKpaM陽撰
【補註】在進行演算時,如果每次運算都予以捨入,
使得在第一個非零數字後(包括此非零數字)不多於3
位數字,就說演算到3位有效數字(51,ific呱di-
gits).從計算(數學中)或測量(科學技術中)中得
到的一個具有;位有效數字的近似數x’=(:、…
:,)xq一”’稱為準確到n位有效數字(n簇T),如果誤差
l((:1…:,)x qr一”一門)一x}
小於qr一”一’/2.通常q=ro或2.例如,0.0308是
杯不石一l=o的準確到3位有效數字的解. |
|
- n.: significant figure
|
|
| 最小有效數字 | 有效數字消去 | 有效數字的概念 | | 保留一位有效數字 | 保留三位有效數字 | 保留兩位有效數字 | | 有效數字的捨入規則 | 有效數字的具體說明 | 有效數字的正確表示 | |
|