幸好高斯把黎曼给坑了！不然就不存在这门神奇的学科了......

Original 超模君 超级数学建模 5/22

按照指示星标置顶

第一时间接收最有料的文章
 

如果将一个带把手的茶杯和一个甜甜圈放在一个人的面前，然后问他：这两个东西有差别吗？

一般人可能会回答：这根本就是两个东西，还需要问有没有差别吗？

但拓扑学家会告诉你：在一个更本质的层面上，这两个东西没有差别。

明明是两个东西，怎么会没有差别呢？
 

因为在拓扑学家的眼中，茶杯和甜甜圈，可以通过这样的变换而变成同一样东西：

是不是觉得很神奇？今天超模君就来讲讲这个被称作“橡皮泥的几何”的学科——拓扑学的前世今生。
 

拓扑学（Topology）是一门研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。也就是说，拓扑学所关注的，并不是传统几何学意义上的面积、体积、形状等一系列的几何特征，而是一种更为基础的“共性”和“个性”。

这种“共性”和“个性”会导致拓扑学对于几何图形和空间的分类，与传统几何的分类完全不一样。在拓扑学中，大小和形状会失去意义（但并非全部），圆、正方形和三角形是等价的——它们之间可以通过连续变换来与对方一样；足球和橄榄球也是等价的。但是足球的表面和游泳圈的表面却不是等价的，这也是为什么说形状并没有失去全部意义的原因。
 

而率先察觉到这种“共性”和“个性”的人，是莱布尼茨。
 

莱布尼茨：终于没有人跟我争了（看着牛顿）
 

然而莱布尼茨觉察到的契机并非来自对几何图形或空间的直接观察，而是来自于对抽象符号的特殊偏好。这种特殊偏好使得莱布尼茨尝试用抽象符号来表示物体几何性质。
 

可是当莱布尼茨有这样的想法时，笛卡尔早已创立了解析几何，用代数来探讨几何性质不再是新奇的东西。

结果莱布尼茨皱了皱眉头，不满道：笛卡尔的方法不好，因为有些几何性质是跟几何体的大小无关的。
 

尽管莱布尼茨察觉到这一点，但他很明显还没想明白到底有哪些几何性质是与几何体的大小无关的（哪怕一条性质也没有给出），以至于他跟很多同时期的数学家提起这个观点时，都是摇摇头，没有给予多少注意。

让莱布尼茨没有想到的是，他的这句话，在三百年之后，被两个后辈发展成为拓扑学的主要内容。

时间来到18世纪，拓扑学在另一个人手里得到了发展——他为拓扑学贡献了两条“最初的定理”。

他的名字，叫做欧拉。

欧拉：身为先驱者就要有这种俯视后辈的气概

欧拉为拓扑学贡献的第一条定理与普鲁士的哥尼斯堡有关。在哥尼斯堡有一个公园，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来（如下图）。有人提出了这样一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点？

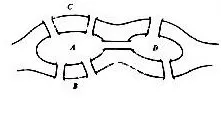
欧拉解决了这个问题，并将它转化成一个“一笔画”的几何问题：如下图中，如何只用一笔，就把整个图形画出来？

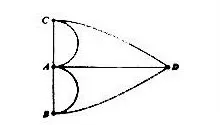
答案是不可能的，因为欧拉给出了这类“一笔画”问题的充分必要条件：奇点的数目必须是0或者2。

所谓“奇点”，就是指连到该点的线段数目为奇数条。“七桥问题”中的四个点均为奇点，按照欧拉提出的充要条件，该问题不可能用“一笔画”来解决。

可以看到，在欧拉转化出来的几何问题中，线段围成的图形形状是不重要的，只需要点的位置关系不改变就行。这就超越了传统几何学的研究范畴，而进入了拓扑学的领域。

欧拉贡献的第二条定理同样超越了传统几何学的范畴：如果一个凸多面体的顶点数为v，棱数为e，面数为f，那么它们f+v-e=2。这个已经与莱布尼茨当初提出的想法相当接近了。

在欧拉之后，高斯于1833年用线积分定义了空间中两条封闭曲线的环绕数，使拓扑学中一个代表性的课题——扭结问题得以发展起来，让拓扑学的内容进一步充实起来。

环绕数：是描述三维空间中两条闭曲线环绕的一个数值不变量。直观上，环绕数表示每一条曲线缠绕另一条曲线的次数。环绕数总是整数，但有可能取正数或负数，取决于这两条曲线的定向。

 

扭结问题：是一个研究如何判断绳子是否打结的课题，即当两段闭合的绳子缠绕在一起时，如何只通过观察，就判断绳子间是否产生扭结的问题。除了判断绳子是否打结以外，还有研究如何给扭结分类的问题。

在数学家们纠结着绳子打结的问题时，一个哥廷根大学的无薪讲师，在他的就职演说中，将现代拓扑学带到了世界上。

这位哥廷根大学的无薪讲师，就是黎曼。

无薪讲师：是指学校不提供固定的薪酬，收入完全来自于听课学生所缴纳的学费的讲师。

黎曼：当个老师还要靠学生打赏来过日子……

不过黎曼的这场就职演说并非是轻松自在，或者说至少准备充足——因为学校委员会在黎曼提交的三个课题中，挑选了黎曼当时没怎么思考过的一个课题——关于几何学的基本假设，来作为他的就职演说主题。
 

这下黎曼就懵了：你们委员会的想法怎么那么独特？我拿了个不怎么成熟的课题来凑个数，你们就看上了？！

加上当时黎曼还颇为贫困，新课题的压力让他一度情绪失控。（心疼黎曼一秒钟）不过最终，黎曼还是用7个星期准备好了演说，而且为了让委员们清楚自己说的是啥，他全场只展示了一个公式，忽略了所有计算细节。尽管如此，委员们依旧表示：

听！不！懂！

万幸的是，还是有人听懂了，这个人就是前面提到的高斯先生。（然而他也是让黎曼情绪失控的罪魁祸首——黎曼的就职演说主题就是他选的）

让我们来看看黎曼到底在就职演说里说了啥：

黎曼认为，几何学的对象缺乏先验的定义，欧几里德的公理只是假设了未定义的几何对象之间的关系，而我们却不知道这些关系怎么来的， 甚至不知道为什么几何对象之间会存在关系。

 

他认为，几何对象应该是一些多度延展的量，体现出各种可能的度量性质。而我们生活的空间只是一个特殊的三度延展的量，因此欧几里德的公理只能从经验导出，而不是几何对象基本定义的推论。欧氏几何的公理和定理根本就只是假设而已。但是，我们可以考察这些定理成立的可能性，然后再试图把它们推广到我们日常观察的范围之外的几何。

 

他给这些多度延展的量取了个名字——德文写作 mannigfaltigkeit, 英文翻译为 manifold，意为“多层”。中国第一个拓扑学家江泽涵将其译作“流形”，即“多样化的形体”。

黎曼还提出了“n维流形”的概念，即流形的局部与 n 维欧氏空间的局部具有相同的拓扑性质，并阐述了关于延展性、维数、以及将延展性数量化的想法。

在黎曼之后，庞加莱继续研究黎曼留下来的n维流形，他创立了用剖分来研究流形的基本方法，同时引进了许多不变量：基本群、同调、贝蒂数、挠系数。不过最著名的，还是他在研究三维流形时留下的“庞加莱猜想”：

任何一个单连通的，闭的三维流形一定同胚于一个三维的球面。

简单的说，一个闭的三维流形就是一个有边界的三维空间；单连通就是这个空间中每条封闭的曲线都可以连续的收缩成一点，或者说在一个封闭的三维空间，假如每条封闭的曲线都能收缩成一点，这个空间就一定是一个三维圆球

到现在为止，拓扑学已经发展出几个成熟的分支：点集拓扑、代数拓扑、同微分拓扑。这些分支学科极大地拓宽了拓扑学的研究范围和研究手段，并且使拓扑学与其他学科产生了意义深远的联系，如物理中的超导现象，就需要拓扑学的理论支持。
 

点集拓扑：有时也被称为一般拓扑学，它研究拓扑空间以及定义在其上的数学结构的基本性质。

代数拓扑：使用抽象代数的工具来研究拓扑空间的数学分支。

微分拓扑：研究微分流形和可微映射的一个数学分支。微分流形除了是拓扑流形外,还有一个微分结构。

也许看到这里，很多模友依旧不能很好地理解拓扑学到底研究的是什么，这并不要紧——因为这是一门异常艰深的学科。而我们现在所需要了解的，是要永远保持一颗求知的心，不要被已有的认知所束缚，就像拓扑学家面对茶杯和甜甜圈时，能够说出的那句话一样：

“在一个更本质的层面上，这两个东西没有任何差别。”