物质究竟是什么？薛定谔是这样说的……

原创 环球科学 环球科学 2019-10-13

1926年，薛定谔提出了可以描述微观粒子运动状态的薛定谔方程（波动方程），创立了波动力学。随后，他证明波动力学与海森堡和玻恩的矩阵力学在数学上是等价的。由于这些贡献，他在1933年与狄拉克共同获得诺贝尔物理学奖。在这篇摘自《环球科学》诺奖专刊的文章中，薛定谔探讨了物质本质是什么——究竟是离散的粒子？还是连续的波？

《环球科学》诺奖专刊涵盖18位诺奖得主的传世经典

点击图片

直达购买页面

何为物质？20世纪初，科学似乎走在通向这一古老问题的明确解答的康庄大道上。看起来，物质最终能被分解为基本的组成要素——某些虽然微小，但切实存在且可以测量的粒子。然而，后来的发展证明，事情没有这么简单。时至今日，物理学家不但没有找到这个问题的答案，甚至还无法再明确区分物质和其他东西了。

我们不能再把物质和力（或者力场）当作对立的不同实体。我们现在知道，这些物理概念是相互交融的，必须合并到一起。诚然，我们仍使用“真空”（即不包含物质的空间）这种说法，但真空实际上是不存在的，空间永远不可能真的空无一物，即便在最遥远的宇宙深处也有星光闪耀，而星光就是物质。此外，空间到处充斥着引力场，依照爱因斯坦的理论，引力和惯性也不能简简单单地分开。

因此，本文的主题实际上是从物理学的角度去理解时空实在性的整体图景。不得不承认，相较以往，我们如今对物质实在性的理解要更加摇摆不定。我们已经知道大量有趣的细节，而且每周都会知道得更多。但是，想要完成一幅清晰、简单易懂且得到全体物理学家认同的整体图景却是一项不可能完成的任务。如今的物理学可以说遭遇了一场严重的概念危机，面对这个危机，很多人丧失了信心，认为根本不可能存在一个客观的实在图景。然而，我们之中的乐天派（包括我自己在内）把这种观点视为在绝望中对哲学的滥用。我们希望，目前的思想动荡仅仅意味着一些陈旧观念的剧变，这样的动荡将引领我们更深入地理解这个学科，最终收获对物质的全面认识，远胜现在手上这一堆零散的公式。

埃尔温 · 薛定谔

离散的粒子

那么，既然我理应描绘的物质图景还并不存在，既然现在还只能看到它的一些碎片，我下面的演讲也许就很难前后一致了。就像塞万提斯的《堂吉诃德》一样——出于健忘，他笔下的桑丘在某一章节里丢掉的驴子过了几章之后竟然若无其事地重新出现，我们今天要讲的故事将同样充满着矛盾。我们将从一个被广泛接受的观点出发，即物质是由大量元胞（或者说原子）构成的，它们的存在已经被许多漂亮的实验证实；与此同时，根据马克斯·普朗克（Max Planck）的发现，能量也是由一种被称为量子的不可分单位组成的，它可以从一个载体突然传递到另一载体。

不过，桑丘的驴子会回来的。后面我会要求你们不要相信元胞是固定不变的个体，也不要相信能量量子的传递是突然的。离散性仍然可以存在，但不是以传统的形式存在，如分立的粒子或者某种突变过程。离散性仅仅作为一种结构出现，这种结构源自某些能够描述相应现象，但尚未被完全理解的物理定律。要找个看得见摸得着的东西做个还算准确的类比的话，那就是铃铛，它的各阶泛音是由铃铛本身的形状及其遵循的弹性定律决定的，但不论是形状还是弹性定律都没有任何固有的不连续性。

物质由基本粒子构成，这一概念最早可以追溯到公元前5世纪的留基伯（Leucippus）和德谟克利特（Democritus），他们把这些基本粒子称为原子。随后，19世纪的詹姆斯·克拉克·麦克斯韦（James Clerk Maxwell）和路德维希·玻尔兹曼（Ludwig Boltzmann）把物质的元胞理论提升到物理实在层面，并应用到气体理论中。从剧烈运动的、不断碰撞和反弹的原子和分子出发，可以导出气体的所有性质：弹性、热学性质、黏度、导热系数和扩散性质。同时，原子概念为热力学理论打下了坚实的基础，即热就是基本粒子的运动，温度越高，运动越剧烈。

20世纪的最初10年可谓成果丰硕，物理学家发现了X射线，发现了电子，发现了原子核通过放射性衰变释放出的粒子流以及其他能量，还得到了各种粒子的电荷。他们随后还精确测量了这些粒子以及它们组成的原子的质量，由此发现了原子核的质量亏损。原子核的质量要比组成它的粒子的质量之和小，这份缺失的质量转化成了结合能，把这些粒子牢固地束缚在原子核中。这被称为堆积效应。束缚核子的核力当然不是电力——电力在这种情况下提供斥力——但比电力强得多，而且只作用于非常短的距离，大约在10^(-13)厘米量级。

这里已经出现了一个矛盾。开头我不是说过，我们不再认为力场和物质存在区别么？我也许可以狡辩说：呃，粒子的力场其实也是粒子的一部分。但事实不是这样。如今公认的观点是，所有东西都既是粒子也是场，既具有我们熟悉的场的连续结构，也有我们熟悉的粒子的离散结构。这个观点得到了无数实验的支持，并且被广泛接受，只是在具体细节上仍有不同意见，正如我们接下来将会看到的。
 

在核力这个例子中，粒子结构我们差不多是清楚的，而连续的力场基本上由所谓的π介子来表示。另一方面，被我们视为离散粒子的质子和中子被晶体衍射时会产生干涉图案，由此可见，它们无疑也具有连续的波的结构。要把这两种截然不同的特性在头脑中组合成一幅图景是很困难的，这也正是导致我们对物质的理解摇摆不定的主要原因。

不论粒子还是波，都不是杜撰的假说。照相乳胶或者威尔逊云室记录下的轨迹毫无疑问地表明了粒子的离散特性。各国国防部正在斥巨资研究核子的人工生产。当然，一个飞驰的粒子本身杀不死人，不然我们早就被消灭殆尽了。但他们的研究有可能间接加速了人类毁灭计划的实现，这与我们每个人都息息相关。

你自己就可以轻松观测到粒子，只需在暗处用放大镜观察腕表上的夜光数字。数字亮度忽明忽暗，像阳光下的湖水一样闪烁。腕表发出的光是由微小亮点组成，每一个都是由放射性原子释放α粒子（氦核）产生的。在这个过程中，释放出α粒子的原子变成了其他种类的原子。探测和记录这类单个粒子可以使用一种叫做盖革-缪勒计数器的特殊装置。限于演讲时间，我不能一一列举各种探测方法了。

连续的波

现在该谈谈连续的场，或者说，物质的波动特性了。我们主要通过衍射和干涉的方法来研究波动结构。对光波的分析和测量主要使用光栅，即表面上蚀刻出大量纤细、平行的等间距条纹的光滑金属。当入射光沿着一个方向照射到光栅上后，会依据波长的不同被散射到不同方向上。但即便是我们所能制造出的最精细的光栅，间隙也依旧太大，无法散射波长非常短的物质波。不过，自从马克斯·冯·劳厄（Max von Laue）首次使用晶格来研究硬X射线，物理学家意识到可以用晶格来散射物质波。高速粒子流照射在晶体表面，就能展现出它们的波动性质。有了晶体光栅，物理学家已经完成电子、中子和质子的衍射实验，并测出了它们的波长。

光的干涉图案，显示了光的波动性质。摄于美国国家标准局，使用汞蒸气产生的光和干涉仪。

电子干涉图案，显示了电子的波动性质。摄于美国无线电公司实验室的晶体衍射实验。

这些和普朗克的量子理论有什么关系呢？普朗克早在1900年就告诉我们，要解释烧红的铁块或者像太阳这种炽热恒星发出的辐射，就必须认为这些辐射是以离散组分的形式产生，并以这种离散形式从一个载体传递到另一载体（比如，从一个原子到另一个原子）。这是极其惊人的，因为在当时，能量仍是高度抽象的概念。5年后，爱因斯坦告诉我们，能量有质量，质量就是能量；换句话说，能量和质量是等同的。现在，当尺度缩小到我们眼睛看不到的程度时，世界的一切都是离散的：我们原来的那些原子、元胞、粒子都是普朗克能量量子。承载能量量子的载体本身也是能量量子。这实在令人头晕。其底层一定有某种根本性的东西，但目前这个秘密还没有解开。这并不让人意外，毕竟，我们研究的尺度也不是突然之间降下来的，降到目前的地步大概花了20~30年，而未来也许还有继续缩小的空间。

接下来的一步虽然跨度没有之前那么大，但仍足够重要。尼尔斯·玻尔（Niels Bohr）巧妙而合理地推广了普朗克假说，他教会我们如何理解原子和分子的谱线，还有原子是怎样由大质量、带正电的核子和环绕在外的小质量、带负电的电子组成。每一个小系统——原子或分子都只能拥有确定的离散能量，具体数值取决于它的性质和组成。在由高“能级”向低“能级”跃迁时，系统会以辐射量子的形式释放多余能量，量子的波长是确定的，反比于量子的能量。这意味着，有确定能量的量子会显现为一种有确定频率的周期过程；过程的频率与能量直接成正比，等于能量除以著名的普朗克常数h。

依照爱因斯坦的理论，粒子的能量等于粒子的质量m和光速c的平方相乘。1925年，路易·德布罗意（Louis de Broglie）提出一个推论：粒子可能总是与一个波动过程联系在一起，波的频率是能量粒子的能量除以h。让他做出如此推断的粒子是电子。过了不到两年，他的“电子波”就被C·J·戴维逊（C. J. Davisson）和L·H·革末（L. H. Germer）的著名电子衍射实验所证实。以此为起点，物理学家意识到所有东西——无一例外——都既是粒子也是波动场。于是，德布罗意的博士论文让我们再难确定物质的本性。粒子图景和波动图景都有揭示真理的价值，我们不能舍弃任何一个。但我们不知道怎样把两者合而为一。

这两种图景是相互关联的，对此我们已经有了充分的认识，这些认识精确度极高，而且深入到了令人赞叹的细节。但是，当要把它们统一成同一幅具体、明白的图景时，各方意见就有了巨大的分歧，以至于许多人认为这种统一是根本不可能完成的。下面我将简要描述一下两种图景的联系，但你不要指望会有一幅统一且具体的图景浮现于眼前，也不要因此责怪我表达能力不足或自己过于愚笨——因为还从未有人成功过。

波有两个独特的性质。第一，它具有波前，前后相继的波前形成了像洋葱皮一样层层叠叠的表面集合。提到波前的二维类比，你一定熟悉石头投入水池中激起的美丽涟漪。第二个特征没那么直观，波存在一条传播路径——与波前垂直的一系列假想的直线。这些直线被称为波“法线”，或者波“射线”。

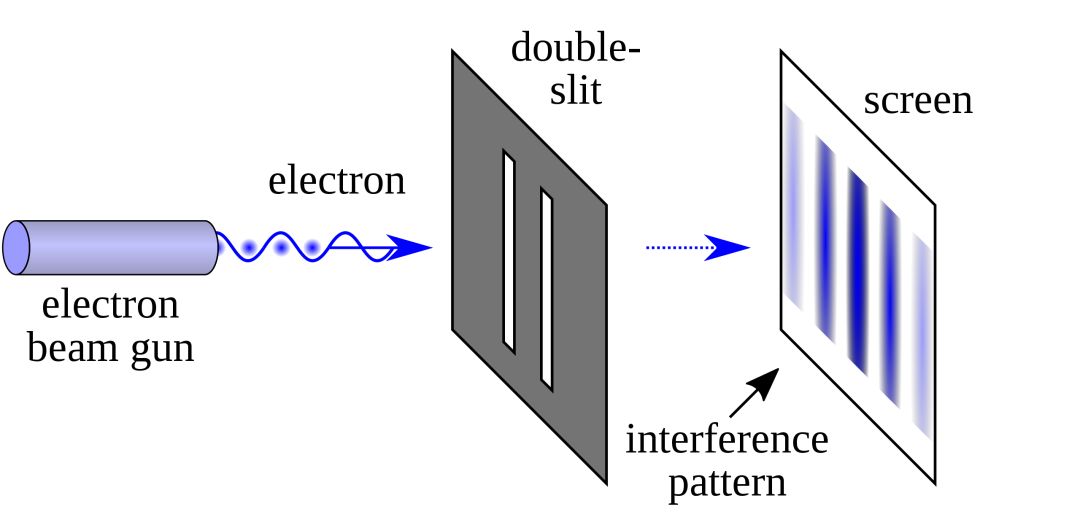
双缝干涉实验。图片来源：维基百科

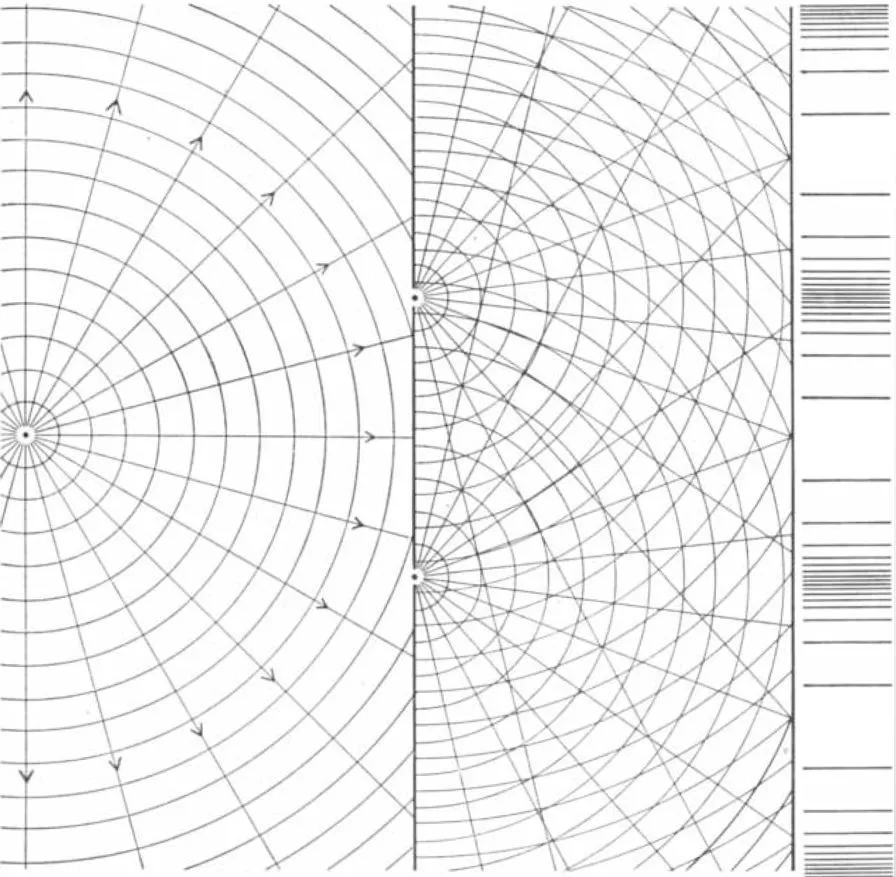
干涉也是波动性的证据。当射线发生交叠时会形成典型图案。

我们可以暂时认为这些射线对应粒子运动轨迹。实际上，如果你沿着波传播的方向，从一束波中切下边长为10或20倍波长的一小块立方体。这个“波包”沿着一条射线运动，其速度及加速度实际上就与波相应的粒子在这个位置的速度和加速度完全一样，如果把作用在粒子上的任何力场也都考虑进去的话。
 

难以调和的图景

我要开始支吾其词了。因为我接下来要说的尽管也是对的，但与这个波粒对应关系几乎是互相冲突的。尽管波包的行为给了我们一个比较直观的粒子图景，甚至在细节上也是合理的（例如，波长变短对应粒子动量增加，这两个量成反比），但出于各种原因，对这个直观图景我们不能太当真。一方面，这个图景毕竟有些模糊，波长越长越是如此。另一方面，我们通常要处理的不是一个小波包，而是范围很大的波。还有，我们必须处理十分重要的特例：能够形成“驻波”的微小“波包元”，它既没有波前也没有波法线。

对波动现象的解释有一个得到众多实验支持的观点：一束均匀传播的波列中，每一点上的相互作用都有二重结构的联系，被称为“纵向”结构和“横向”结构。横向结构对应波前，在衍射和干涉中显现；纵向结构对应波法线，在单粒子观测实验中显现。然而，这些结构的定义并不精确，也不绝对，因为波前和波法线的定义本身就不是非常精确。

这种纵向、横向结构的解释在驻波情形下彻底失效了。在这里，整个波动现象都局限在很小的区域，只有一个或几个波长的尺度。你可以在水盆里制造出驻波，只要用手指在水盆中央有节奏地点击水面，或者直接轻推水盆让水面波动起来。这种情况下我们处理的不是均匀传播的波；真正值得注意的是这些驻波的简正频率。水盆里的水波可以类比电子波动现象，而后者发生在原子尺度的区域内。在原子核周围涌动的波群，它们的简正频率精确地等于玻尔原子“能级”除以普朗克常数h。于是，原子的玻尔模型连同旧的量子理论一起被德布罗意的波动解释取代了。前者虽然精巧但多少有些人造痕迹，而后者要自然得多。波动现象构成原子的“身体”，它代替了玻尔模型中那些围绕原子核旋转的点状电子。点粒子在原子中没有存在的可能，所以如果有人仍然把核子看作点粒子，他一定是出于权宜而有意这样做的。

在我看来，“能级”就是振动简正模的频率，这一发现的最重要意义就是让我们可以放弃突然跃迁 （或者说量子跳跃）的假设，因为两个或者多个简正模完全可以同时激发。我相信，简正频率的离散性足以解释普朗克考虑的问题以及其他类似的、同等重要的问题了——我指的是整个量子热力学。

氢原子光谱和解释氢原子光谱的玻尔理论。图片来源：维基百科

随着时间的推移，量子跳跃理论变得越来越让人难以接受，至少对我而言是这样。但是放弃这套理论将导致影响深远的后果。如果没有量子跳跃理论，我们就必须完全放弃能量以确定的量子为单位进行交换的构想，代之以振动频率之间共振的概念。然而我们已经看到，由于爱因斯坦的质能关系，我们必须把粒子看成普朗克能量量子。这听起来让人害怕，因为这个替代理论指出，我们不能再把单个粒子看成有着良好定义的不变实体了。

实际上，也没有其他方法能定义粒子个体。一方面，沃纳·海森堡著名的不确定原理指出，粒子不能同时具有明确定义的位置和速度。这种不确定性意味着我们无法断定同一个粒子是否能被观测两次。粒子不能被区分还有另外一个决定性原因，就是当我们考虑两个或多个同种类粒子相互作用时，比如氦原子中的两个电子，这些粒子的个体特征必须要抹除掉。如果存在两种状态，它们的区别只是交换了那两个电子，那么必须认为这两种状态是同一个，否则就会得到无意义的结果。这种论证毫无例外的适用于任意种类和任意数量的粒子。

多数理论家应该会接受上面的推导，并且承认粒子的确不是定义良好的不变实体，不存在可测的个性或共性。但是，可区分的粒子这种概念仍然在他们的理论和讨论中扮演重要角色。更加根深蒂固的是对“量子跃迁”的信仰，这个概念现在已经被一套玄奥难懂的术语所包围。举个例子，量子理论的现行词汇里有一个重要词语叫“概率”，描述的是从一个能级到另一能级的跃迁。但是，要说某件事的概率有多大，就得先假设它确实有可能发生。如果跃迁发生了，那它一定是立刻完成的，因为没有中间过程存在。如果跃迁需要时间，可以想见，它就有可能被意外的干扰打断。这种可能性真是让人茫然。

解决波粒二象性困境的方法之一，是仅仅把波场当作计算手段，用来得到粒子在某个位置出现的概率。然而，一旦把波的实在性去掉，只把它当作提供信息的手段，那么，从粒子角度理解干涉和衍射现象将变得异常困难。与其从粒子角度解释波动现象，不如从波的角度解释粒子的轨迹，这样显然更简单些。

诚然，“真实的存在”这种说法已经被哲学家反复探讨了不知多少次，但它简单、原始的含义已经无从考据了。因此我想回忆一些其他事情。我说过，元胞没有个体特征。可以说，人们从来没有两次观测过同一个粒子——就像赫拉克利特（Heraclitus）说的不能两次踏入同一条河流。你无法标记一个电子，你也不能把它涂成红色。实际上，你都不能想象电子被标记；如果你这样做了，你将得到错误的计数，你的计算每一步都是错的——无论是计算光谱的结构，还是在热力学和其他什么领域。而另一方面，波可以被轻松赋予个体特征，从而被清楚地识别出来。想象一下引导海上船只的灯塔，它的光按照特定编码闪烁，比如：亮3秒钟、暗5秒钟、亮1秒、再暗5秒、然后再亮3秒——船长就会知道已经到达圣塞瓦斯蒂安了。或者你用无线电话与大西洋彼岸的朋友通话，当你听到对方说，“你好，我是爱德华·梅尔，”你知道他的声音已经在无线电波上印刻下了可以被清楚地识别，与其他无线电波不同的结构。其实也不必跑那么远。当你的妻子从花园里喊“弗朗西斯”的时候，道理是一样的，只是结构印刻在声波上，且距离短了些（但花费的时间却比无线电穿越大西洋的时间还要长）。我们所有的口头交流都是基于具有个体特征的波动结构。除此之外，依照同样的原理，电影和电视给我们传递了多少丰富的细节信息呀！

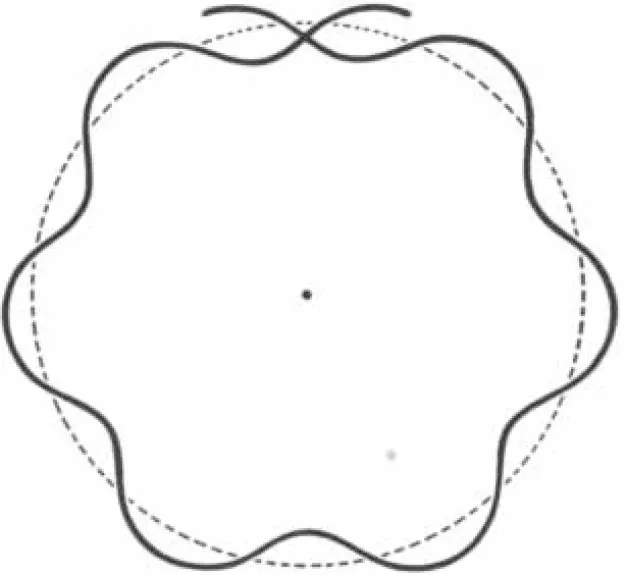
在波动力学看来，电子不是原子中的点状物体，而是在原子中来回涌动的驻波。有些振动模式是可以存在的（上图），而另外一些则不可能（下图）。可存在的振动模式的精确对应玻尔理论的能级。

这种波动现象的个体特征，在更加精细的粒子波上面也有非常多的体现。只需举一个例子。一团有限体积的气体，比如氦气，既可以理解成大量氦原子的集合，也可以理解成基本的物质波列的叠加。两种角度都能得到相同的理论结果，正确描述气体在加热、压缩以及其他情况下的行为。但如果你尝试对气体进行某种复杂的枚举，你必须依照不同的理解方式而采取不同的策略。如果你把气体当作粒子，那么就像我说过的，不要给这些粒子赋予个体特征。如果你把气体当作物质波列的叠加，那么每一个波列都具有定义良好的结构，使之与其他波列区分开来。当然，有许多波是非常相似的，把它们交换一下对气体也不会有明显影响，但如果你真把这些相似的状态当作同一种状态，你得到的结果将会错得离谱。

我们终究不能把量子跳跃和具有个体特性的元胞这类概念完全驱逐出物理学。我们仍然需要它们来描述物质结构的诸多细节。如果不接受粒子是相当具体而真实的东西，怎么能以极高的精度测出碳核和氢核的质量，并发现碳核要比12个氢核的质量之和稍小一些？粒子图景在这里要比波动图景方便太多，我们不能不用它。就像化学家不能丢掉价键公式，即便他已经充分认识到这些公式只是复杂的波动力学的过分简化。

如果最后你问我：“所以，这些元胞到底是什么呢？”我必须坦白，我没有准备好这个问题的答案，就像我不知道桑丘的驴子是如何失而复得一样。我最多只能说，你可以把粒子看成波场中临时性的实体，因为波动定律清楚、明确地决定了波场的形式和一般行为，所以在许多过程中这些临时性的实体看来就像始终存在的东西一样。在高精度下，粒子的质量和电荷必须用波动定律决定的结构因子来计量。而宏观的电荷守恒和质量守恒由“大数定律”推出，必须被看作是一种统计效应。

撰文：埃尔温 · 薛定谔（Erwin Schrödinger） 

翻译：苏洪轶
 

审校：陈景灵